Tensor network and its contractions

This page serves as documentation for our main tensor network contraction engine.

Overview

Tensor Valued Objects

A tensor is a multi-dimensional array of numbers. The number of dimensions associated to a tensor is called the rank of the tensor. For example, a tensor of rank 0 represent a scalar \(T\). A tensor of rank 1 is a vector \((T_i)_{i=0}^{d-1}\), and a tensor of rank 2 is a matrix \((T_{ij})_{(i,j)\in [d_0]\times [d_1]}\). The dimension corresponds to each of the indices are called bond dimensions associated to the indices.

A tensor network represents a multi-linear map of multiple tensors that results in a new tensor. For example:

• The inner product of two vectors \(U, V\) can be expressed as \(T = \sum_i U_i\cdot V_i\).

• The outer product of two vectors \(U, V\) can be expressed as \(T_{ij} = U_i\cdot V_j\).

• The element-wise product of two vectors \(U, V\) can be expressed as \(T_i = U_i\cdot V_i\).

• The matrix product of two matrices \(M, N\) can be expressed as \(T_{ij}=\sum_k U_{ik}\cdot V_{kj}\).

Explicit expressions like above are good for sake of demonstrations, but more complex tensor networks could arise from various scenarios, including many-body physics, machine learning and quantum computation. There are several equivalent ways of expressing a tensor network:

• Einstein summation. An einstein summation takes the form [indices_0],[indices_1],…,[indices_k]->[indices_o]. Each term on the left hand side corresponds to the indices configuration of an operand, and the indices on the right hand side corresponds to the indices on the right hand side, also called the open indices. All matching indices are identified with each other, and the closed indices, i.e. the ones that do not appear on the right hand side, are being summed over. The four examples above, expressed in terms of the Einstein summation, are respectively i,i->, i,j->ij, i,i->i, ik,kj->ij. There is a more restrictive interpretation of the einstein summation that each index appears exactly twice in the expression and the right hand side is thus removed. We do not take such convention. Moreover, each edge can appear multiple times on the right hand side, and does not have to appear on the left hand side as long as each index is associated with a definite bond dimension.

• Attributed Multi-hypergraph. A tensor network can be expressed as a multi-hypergraph, where each node corresponds to a tensor operand, and each hyperedge an index. This provides a graphical, intuitive representation of a tensor network.

Our package not only supports the definition and manipulation of tensors and tensor networks, but also unary functions acting on a tensor and summation of tensors with the same shape. These extensions help us handle different scenarios where tensors appear naturally in an easier manner.

class acqdp.tensor_network.TensorValued(*args, **kwargs)

Interface for all TensorValued objects, including Tensor, TensorNetwork, TensorSum and TensorView.

Variables

• identifier – unique identifier for each TensorValued object.

• dtype – A TensorValued object is homogeneous, and contains elements described by a dtype object.

property shape

The common property of all TensorValued classes, indicating whether the bond dimensions for a tensor valued object. A tensor valued object is semantically a multi-dimensionally array, and its dimensions can be expressed as a tuple of integers. The tuple is called the shape of the tensor, whereas the length of the tuple is the rank of the tensor.

In ACQDP, undetermined tensors and undetermined dimensions are allowed. In the former case, the shape of the tensor will return None; in the latter case, some of the bond_dimensions appearing in the tuple could be None.

Returns

tuple or None

Raises

NotImplementedError, ValueError

property is_valid

The common property of all TensorValued classes, indicating whether the TensorValued object is valid or not. In every step of a program, all existing TensorValued object must be valid, otherwise an exception should be thrown out.

Returns

bool

Raises

NotImplementedError

property is_ready

The common property of all TensorValued classes, indicating whether the current TensorValued object is ready for contraction, i.e. whether it semantically represents a tensor with a definite value. A TensorValued object needs to be ready upon contraction, but needs not to be ready throught the construction.

Returns

bool

Raises

NotImplementedError()

fix_index(index, fix_to=0) → acqdp.tensor_network.tensor_valued.TensorValued

Fix the given index to the given value. The result TensorValued object would have the same type as the original one, with rank 1 smaller than the original.

Parameters

• index (int) – The index to fix.

• fix_to (bool) – the value to assign to the given index.

Returns

TensorValued – The TensorValued object after fixing the given index.

Raises

NotImplementedError

contract(**kwargs) → numpy.ndarray

Evaluate the TensorValued object to a numpy.ndarray.

Returns

numpy.ndarray

Raises

NotImplementedError

cast(dtype)

Cast the tensor valued object to a new underlying dtype.

class acqdp.tensor_network.Tensor(*args, **kwargs)

Bases: acqdp.tensor_network.tensor_valued.TensorValued

A Tensor is an array of numbers with multiple dimensions. The most basic examples of a Tensor are a vector (1-dimensional arrays of numbers) and a matrix (2-dimensional arrays).

In our implementation, Tensor is a subclass of TensorValued, where the value is stored in an numpy.ndarray. All other TensorValued represent operations over the Tensor objects.

Variables

_data – numpy.ndarray object representing the data corresponding to the tensor.

__init__(data: numpy.ndarray = None, dtype: type = <class 'complex'>) → None

Constructor of a Tensor object.

class acqdp.tensor_network.TensorSum(*args, **kwargs)

Bases: acqdp.tensor_network.tensor_valued.TensorValued

A TensorSum object represents the summation of multiple tensors.

Variables

terms_by_name – a dictionary with key-value pairs, where the key is the name of a summand and the value is the corresponding summand TensorValued object.

__init__(terms=None, dtype: type = <class 'complex'>) → None

The constructor of a TensorSum object.

add_term(term=None, tensor=None)

Add a term to the summation.

Parameters

• term (hashable) – Name of the term to be added. If not given, an auto-assigned one will be given as the output.

• tensor (TensorValued or None) – Value of the term to be added.

Returns

The name of the newly added term.

update_term(term, tensor=None)

Update the value of a term in the summation.

Parameters

• term (hashable) – Name of the term to be updated.

• tensor (TensorValued) – New value of the term

Returns

Name of the term to be updated.

remove_term(term)

Remove a term from the summation.

Parameters

term (hashable) – Name of the term to be removed.

Returns

TensorValued Value of the removed term

class acqdp.tensor_network.TensorView(*args, **kwargs)

Bases: acqdp.tensor_network.tensor_valued.TensorValued

TensorView is a subclass of TensorValued representing unary operations over another TensorValued

object that preserves the shape of the tensor. Common examples include element-wise conjugation and normalization with respect to the frobenius norm.

Variables

• tn – the underlying TensorValued object where the unary operation is performed onto.

• func – the unary function to be applied.

• homomorphism – indicator whether the unary function is homomorphic to the addition and multiplication of tensors. If so, the unary function can be broadcast to lower-level tensors, enabling potential simplification of the tensor network structure.

• dtype – dtype for the tensor entries.

__init__(tn, func=<ufunc 'conjugate'>, homomorphism=False, dtype=<class 'complex'>)

The constructor of a TensorView object.

class acqdp.tensor_network.TensorNetwork(*args, **kwargs)

Bases: acqdp.tensor_network.tensor_valued.TensorValued

A TensorNetwork is a collection of Tensor, with indices from different tensors identified and summed up to present a new tensor. An example of tensor network is two 2-tensors with a common edge representing the matrix multiplication. A TensorNetwork is a graphical representation of an Einstein summation.

Variables

• network – attributed networkx.Graph object, representing the attributed hypergraph of the tensor network as a tanner graph.

• dtype – dtype of the TensorValued object.

• open_edges – a list of edge names, indicating the outgoing wires of the tensor network.

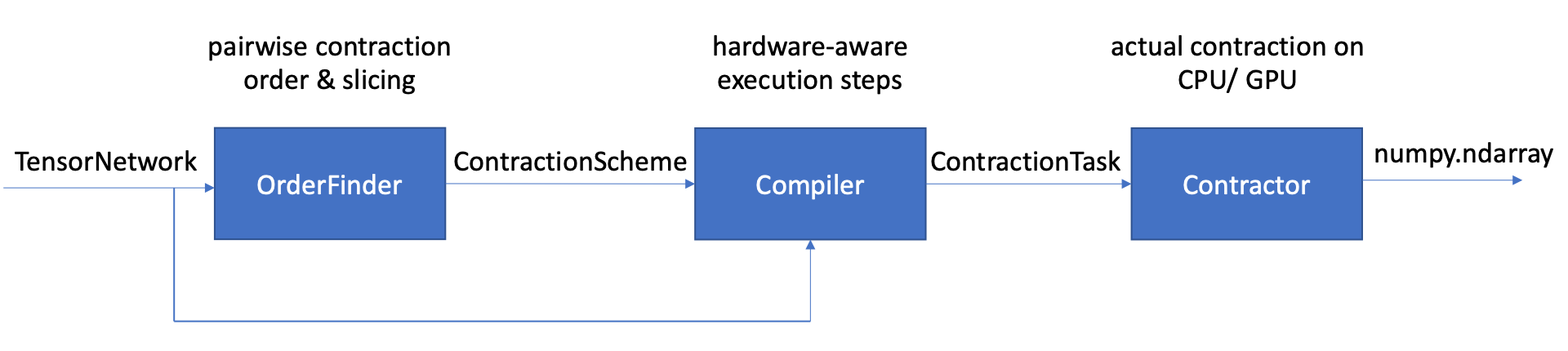
contract(preset=None, config=None, **kwargs)

Evaluate the TensorNetwork object as an numpy.ndarray.

Parameters

• preset (“default”, “khp” or None.) – Select a preset mode. If set to default, will contract the tensor network with default ordering and no post-processing. If set to khp, will invoke advanced KaHyPar-based contraction order finding routine. If set to None, will read config file or input keyword arguments for order finding specifications.

• config (str) – File name for the config file. If preset option is not given and config file is given, the keyword arguments will be ignored and the specification will be read from the config file.

• kwargs (dict) – If neither the preset option nor the config file name is given, the program will read the keyword arguments for order finding specifications. See OrderFinder, Compiler, Contractor for individual specifications.

Returns

numpy.ndarray.

find_order(input_file=None, output_file=None, **kwargs)

Find a contraction scheme of the TensorNetwork object. Equivalent to next(get_order_finder(**kwargs).find_order(self)). See OrderFinder.find_order().

Parameters

• input_file (str, optional) – Input file name. When given, load the contraction scheme from the input file.

• output_file (str, optional) – Output file name. When given, the contraction scheme found will be dumped into the file.

Returns

ContractionScheme

compile(order, **kwargs)

Compile a ContractionScheme corresponding to the TensorNetwork object into a runtime executable contraction process as a ContractionTask. Equivalent to Compiler(**kwargs.get(‘compiler_params’, {})).compile(self, order) (See Compiler.compile()).

Returns

ContractionTask

add_node(node_name=None, edges=None, tensor=None, is_open=False)

Add a node into the tensor network.

Parameters

• node_name (hashable) – The name of the node to be added. If not provided, a new name will be assigned.

• edges (List – list of edges in the tensor network corresponding to the open edges of the new node. If not given, defaults to edges [0, …, len(shape)]) – The edges the new tensor node is being connected to.

• tensor (tensor_network.tensor_valued.TensorValued.) – The value of the newly added tensor.

• is_open (bool) – Whether the new indices associated to the new node will be added to open_edges.

Returns

hashable – Name of the node added. If none is given as input, return the one automatically signed.

Raises

ValueError – An existing node in the tensor network is being added.

Raises

IndexError – A node is added with ambiguous connection to the tensor network. Happens when neither the shape of the tensor nor the connecting edges are given.

Raises

AssertionError – A mismatch in the bond dimensions.

pop_node(node_name)

Pop a tensor node from the tensor network. This operation simply removes the node from the hypergraph.

Returns

dict – The dict containing all the information of the popped node, including its tensor and hyperedge connections.

Parameters

node_name (hashable) – Name of the node to be popped.

remove_node(node_name)

Remove a tensor node from the tensor network. The difference between removing a node and popping anode is that popping a node does not change the output shape of the tensor network, while removing a node would result in a new tensor-valued object, where all edges connected to the removed node are appended to the end of the open edges list.

Returns

dict – The dict containing all the information of the removed node, including its tensor and hyperedge connections.

Parameters

node_name (hashable) – Name of the node to be removed.

update_node(node_name, tensor=None)

Update an existing node of the tensor network by another tensor-valued object.

Parameters

• node_name (hashable) – Name of the node to be updated.

• tensor (TensorValued or None) – The new tensor to be put at the node. If None, the tensor must be updated with an actual value later in order for the tensor network to be ready for contraction.

Raises

AssertionError – Node update results in a bond dimension mismatch.

add_edge(edge_name=None, bond_dim=None)

Generate an index which is not in this tensor network before.

Parameters

• edge_name (hashable) – Name of the edge to be added. Will be automatically assigned if none is given.

• bond_dim (int or None) – Bond dimension of the edge. If set to None, the edge bond dimension will be wildcard until set otherwise.

Returns

hashable – Name of the newly added edge.

open_edge(edge_name=None, bond_dim=None)

Append an edge to the list of open edges. If the edge does not exist, it will be created.

Parameters

• edge_name (hashable) – Name of the edge to be opened.

• bond_dim (int) – Bond dimension of the edge. See add_edge.

close_edge(edge_name)

Make an edge closed. All appearances of the edge will be removed from the open edges list.

Parameters

edge_name (hashable) – Edge to be closed.

fix_edge(edge_name, fix_to=0, change_fix=False)

Fix an edge to a fixed value. The tensor network structure is not yet modified; this method only puts an attribute to the fixed hyperedges. The structure will be changed upon calling the fix method.

Parameters

• edge_name (hashable) – Edge to be fixed to a specific value.

• fix_to (int) – the value the edge is fixed to. Should be an integer ranging from 0 to bond_dim - 1.

• change_fix (bool) – Mode of fix_edge. If change_fix is set to True, the edge will be fixed to the given value regardless of how it is fixed previously. If set to False, the fix will apply together with the previous fix, resulting in a zero tensor if the two fixes do not match.

merge_edges(edges, merge_to=None)

Merge a list of edges as one single edge by identification.

Parameters

• edges (List) – The list of edges to be merged into one.

• merge_to (hashable) – The name of the edge all the edges are merged to. If set to None, the merged edges will appear as edges[0]

rewire(node_name, leg, rewire_to=None)

Rewire an outgoing edge of a tensor node to another edge in the tensor network.

Parameters

• node_name (hashable) – Name of the tensor node for whom an outgoing edge is to be rewired.

• leg (int) – Index of the outgoing edge regarding the tensor node. Should be an integer ranging from 0 to rank(t) - 1, t being the corresponding tensor.

• rewire_to (hashable) – The edge name in the tensor network to redirect the leg to. If None, it will be rewired to a newly created edge.

Tensor Network Contraction Related

Given the tensor operands and the network hypergraph as inputs, tensor network contraction aims to evaluation of the tensor network. Tensor network contraction is a computationally hard problem (\(\#P-complete\)), but cleverly contracting intermediate-sized tensor networks are of great interest.

Our packages aims at efficient exact tensor network contraction, i.e. no approximation is made throughout the process. The contraction process consists of the following steps: order finding, runtime compilation and contraction.

Order finding

One way of tensor network contraction is to merge two tensor nodes into one at a time, until only one tensor is left as the outcome. The cost for such method is determined by the stepwise cost. Such method can be formulated as a binary contraction tree with each node representing a pairwise contraction step. Our algorithm uses the method first introduced in [GK20] to construct efficient contraction trees using hypergraph decomposition. A preliminary order finding scheme is given in OrderFinder when the tensor network is relatively small. More advanced, hypergraph-decomposition-based order finding approach is given in KHPOrderFinder.

Sometimes, a fully serialized contraction tree can be too costly to be carried out due to time / space constraints; for a complex tensor network, it is possible that whatever contraction tree one finds would result in an intermediate result that is well beyond the space of a laptop. We introduced the idea of index slicing in [CZH+18] for parallelization that helps both on running the contraction scheme concurrently, and on relieving the hard space constraint. The slicing method is provided in the class Slicer, and integrated to the order finding scheme as SlicedOrderFinder.

As a result of its execution, a call to find_order would yield ContractionScheme.

class acqdp.tensor_network.ContractionScheme(order, slices=None, cost=None)

ContractionScheme is an intermediate representation of a tensor network contraction, containing the pairwise

contraction orders, the hyperedges to be sliced, and the cost of the contraction. A ContractionScheme does not contain tensor data.

Variables

• order – The pairwise sequential contraction order.

• slices – The hyperedges to be sliced for parallelism.

• cost – ContractionCost – The time / space cost and number of sub-processes of the tensor network contraction.

class acqdp.tensor_network.OrderFinder(order_method='default', **kwargs)

OrderFinder class is dedicated to finding a contraction scheme corresponding to a given tensor network structure.

The main method of an OrderFinder is find_order, which takes a TensorNetwork as input, and yields a generator of ContractionScheme.The base class offers preliminary order finding schemes. For more advanced hypergraph-based approach, use KHPOrderFinder. For finding contraction schemes with sliced edges, use SlicedOrderFinder.

Variables

order_method – ‘default’ order contracts the tensor one by one by order; ‘vertical’ order contracts the tensor based on the vertical ordering. When the tensor network is from a quantum circuit, the vertical order corresponds to the tensor network contraction where the tensors connected to a qubit is first contracted together and then merged to a main one according to a given order of the qubits.

find_order(tn, **kwargs)

Find a contraction scheme for the input tensor network subject to the constraints given in the OrderFinder.

Parameters

tn (TensorNetwork) – A tensor network for which the contraction scheme is to be determined.

Yields

A ContractionScheme containing the pairwise contraction order, a list of edges to be sliced, and optionally the total contraction cost.

class acqdp.tensor_network.KHPOrderFinder(num_threads=28, num_iters=50, num_cmas=1, cma_args=<dict>, eps=None, **kwargs)

Bases: acqdp.tensor_network.order_finder.OrderFinder

KHPOrderFinder utilizes hypergraph decomposition and cma-es opmization scheme for finding contraction orders for

intermediate-size tensor networks.

Variables

• num_threads – Number of threads to concurrently search for the best order.

• num_iters – Number of iterations for cma optimization.

• num_cmas – Number of times cma-es optimization scheme is called for exploring better parameter combinations.

• cma_args – Arguments for cma-es optimization scheme. See the documentation of cma for more details

• eps – In case a good parameter combination is already known, inputting a eps would skip the cma optimization scheme and directly yield orders found by hypergraph decomposition.

class acqdp.tensor_network.SlicedOrderFinder(base_order_finder={'order_finder_name': 'khp'}, slicer={'slicer_name': 'default'}, num_candidates=20, **kwargs)

Bases: acqdp.tensor_network.order_finder.OrderFinder

Class

SlicedOrderFinder finds a sliced contraction scheme based on unsliced contraction schemes found by its base order finder.

Variables

• base_order_finder – The base order finder of the sliced order finder, from which the SlicedOrderFinder fetches contraction schemes and do slicing on it.

• slicer – The slicing algorithm acting upon the contraction schemes.

• num_candidates – Number of unsliced contraction schemes to feed to the slicer at a time. Set to 20 by default.

class acqdp.tensor_network.Slicer(num_iter_before=0, num_iter_middle=20, num_iter_after=100, max_tw=29, max_num_slice=- 1, num_threads=28, slice_thres=0.02, **kwargs)

Slicer finds slicing of an unsliced contraction scheme when called by the SlicedOrderFinder.

Variables

• num_iter_before – Number of iterations of local optimization before slicing.

• num_iter_before – Number of iterations of local optimization in the middle of slicing.

• num_iter_before – Number of iterations of local optimization after slicing.

• max_num_slice – Maxmimum number of edges to be sliced. If set to -1, the constraint will be ignored.

• num_threads – Number of threads for multi-processing.

• slice_thres – Automatically slice edges that introduce an overhed below this threshold. Set to 0.02 by default.

class acqdp.tensor_network.MPSlicer(num_iter_before=0, num_iter_middle=20, num_iter_after=100, max_tw=29, max_num_slice=- 1, num_threads=28, slice_thres=0.02, **kwargs)

Bases: acqdp.tensor_network.slicer.Slicer

Multi-processing slicing, by concurrently trying different slicing routes.

class acqdp.tensor_network.LocalOptimizer(size=13, **kwargs)

LocalOptimizer takes a pairwise contraction tree and do local optimization on the tree. Note that a connected

subgraph of the contraction tree represents a sequence of intermediate steps that take some (potentially intermediate) tensors as input, and outputs a later intermediate tensor. This sequence of steps can be optimized based on solely the shapes of the input and output tensors associated to the subgraph, without looking at the rest of the contraction tree. This allows local reorganization of the tree.

Each iteration of local optimization consists of two steps: In the first step, the contraction tree is divided into non-overlapping subgraphs each up to a given size, with the internal connections in the subgraphs removed. The internal connections are then reconstructed in the second phase using accelerated optimum contraction tree finding approach. The iterations can be repeated by each time randomly selecting a different patch of subgraph division.

Variables

• size – The maximum number of nodes to be included in one subgraph.

• resolver – The resolver to help reconstruct the pairwise order from subgraph divisions.

Runtime-specific optimizations

A good contraction scheme involving sliced edges and pairwise contraction order might seem appealing in theory, but further work needs to be done for fully unleash the potential of the hardware to carry out such contraction efficiently. The Compiler aims to minimize the inefficiencies introduced by small-tensor operations, which take up a majority of number of steps and can not make full use of the existing hardwares. More specifically, Compiler does the following processing to increase the overall efficiency.

• Pre-computation. A typical contraction order has a stem-branch structure, i.e. it consists of a majority of small tensor multiplications (i.e. branches), and a few operations involving a big tensor obsorbing small tensors step by step (i.e. the stem). It is often the case that the stem requires too much memory that slicing becomes necessary, but the branches would need to be computed many times as a result. Although this does not add too much in the theoretical cost, it takes up a large amount of total time. To avoid this, Compiler moves the small tensor multiplications before slicing. As it only has to be done ones prior to all slicing, the inefficiencies caused by small tensor operation is almost entirely reduces. These small tensor operations are then called pre-computation as they happen before slicing and the contractions on the stem.

• Branch merging. A typical contraction step on the stem is that the stem tensor (typically a big one) absorbs a small one as a result of contracting the corresponding branch. The branch tensor is sometimes so small that the multiplication cannot make full use of the GPU to achieve high-efficiency tensor contraction. One way to get around this is to slightly relax the floating point operations constraint, and merge two adjacent tensors together to form a bigger tensor, and then contract it to the stem.

class acqdp.tensor_network.ContractionTask(output, inputs=None, commands=None, data=None, length=1, shape=None, fix_dict=None, open_edges=None, sub_outputs=None, cnt=0, dtype=<class 'complex'>)

ContractionTask is post-compilation intermediate representation for tensor network contraction, with all the

information necessary to carry out a tensor network contraction, including initial tensor data and stepwise instruction of the contraction.

execute(**kwargs)

Execute a ContractionTask.

Equivalent to Contractor(**kwargs).execute(self)().

class acqdp.tensor_network.Compiler(reorg_thres=23, patch_size=5, do_patch=False, **kwargs)

Compile a ContractionScheme indicating contraction scheme and sliced edges into a ContractionTask, a hardware-aware format that can be readily used for tensor network contraction.

Typically, a ContractionScheme found by one of the OrderFinder only aims to minimize the theoretical floating number operations and / or largest size of intermediate tensors. Although those are typically accurate indicators of the overall contracion cost, they fail to accomodate inefficiencies from elsewhere. The compiler takes care of machine-related inefficiencies by slightly modifying the order.

Variables

• do_patch – If set to false, the patching and reorganization of the contraction order below will be skipped.

• patch_size – Whenever two adjacent branches both have size less than the patch size, the branches are merged together. This is to avoid inefficiency called by skewed tensor shapes in tensor multiplication, with a slight sacrifice in floating number operations.

• reorg_thres – Threshold for contraction order reorganization. The order is seperated into small tensor multiplications and large tensor multiplications. All pairwise tensor multiplications involving tensors with size less than reorg_thres will be put forward whenever possible.

compile(tn, scheme, **kwargs)

Parameters

• tn (TensorNetwork) – The TensorNetwork the input contraction scheme is based on.

• scheme (ContractionScheme) – The contraction scheme from which the task is generated.

Returns

ContractionTask – The compiled contraction task ready for execution.

Contraction

Finally, Contractor makes use of GPU, with the help of jax and opt_einsum to further increase the efficiency.

class acqdp.tensor_network.Contractor(exeEngine=None, backend='default', dtype=<class 'complex'>, **kwargs)

Contractor class for tensor network contraction takes a ContractionTask object and execute it sequentially. For NetworkContractionTask, multi-processing is available for further accelarate the computation.

Variables

• backend – When set to jax, large tensor contractions will make use of the jax backend. numpy.einsum is used otherwise.

• exeEngine – Extension interface for other contraction backends. Set to None by default. When set to parallel, subtasks will be computed simultaneously.

execute(tasks, lst=None, **kwargs)

Execute a contraction task.

Parameters

• tasks (acqdp.ContractionScheme) – The task to be executed.

• lst (List) – The list of subtasks to be executed. If set to None, all subtasks are executed and merged together.

Returns

numpy.ndarray – Final result expressed as a multi-dimensional array.

References

GK20

Johnnie Gray, and Stefanos Kourtis, Hyper-optimized tensor network contraction, arXiv preprint arXiv:2002.01935, 2020.

CZH+18

Jianxin Chen, Fang Zhang, Cupjin Huang, Michael Newman, and Yaoyun Shi, Classical simulation of intermediate-size quantum circuits, arXiv preprint arXiv:1805.01450, 2018.